Dr Amit N. Jinabhai is a Senior Lecturer in Optometry, working in the Faculty of Biology, Medicine and Health. He won a Teaching Excellence Award (2021) for his ability to teach challenging content in innovative and engaging ways, to positive effect on both student feedback and performance, earning him Honorary Fellowship of the University’s Institute of Teaching and Learning. Amit is also a former winner of the Association of Optometrists (AOP) ‘national’ Lecturer of the Year Award. Amit was also awarded ‘Division Teacher of the Year 2021’ for the Division of Pharmacy and Optometry. 

 

Introduction 

Like many academics, one of my biggest challenges in recent years has been designing open-book, on-line summative examinations that were robust against both collusion and plagiarism. 

From a broad pedagogical point-of-view, summative assessments (SAs) differ greatly from formative assessments, in that SAs typically: 

• Occur at ‘a fixed point in time’ only, most likely at the end of an instructional period of learning,  
• Are designed to assess the unit’s intended learning outcomes (ILOs), which can often serve as a helpful standard, or ‘benchmark’, 
• Are ‘high-stakes’ assessments, in that they substantially contribute to the final grade for that unit, 
• Are helpful for ranking student performance against their peers, 
• Assist a programme team in identifying students who are not performing at the appropriate level, 
• Assist a programme team in identifying students that should be permitted to progress onto the next stage of study. 

 

My dilemma  

Most units on the Optometry programme, on which I primarily teach, were amenable to on-line, essay-based SAs that were submitted through TurnItIn to check for plagiarism and/or potential collusion. In stark contrast, my four units are centred on ILOs that are unsuitable for essay-based SAs, as they predominantly involve calculations. This led me to carefully reflect on a key question … if I want to set questions on an open-book SA, which are based on calculations, how am I going to prevent my students from potentially colluding? 

Conceptualisation of a valid approach 

Initially I researched and considered various methods that had previously been used to prevent collusion and other forms of academic malpractice in open-book SAs. I also discussed my concerns with colleagues outside of the University. Through my research and  discussions, I decided on four important approaches that I believed to be practicable and deliverable: 

• Randomisation of the order of the questions, 
• Setting a defined ‘assessment window’ time-period, beyond which the exam cannot be started nor submitted, 
• Preventing back-tracking to previously answered questions, 
• Setting a defined exam ‘expiry’ time-period, beyond which the exam gets ‘cut-off’ and automatically submitted. 

I chose to use Blackboard as my platform for delivering my SAs for each of my different units, as it enabled implementation of all four approaches simultaneously.  

Calculated Formula Questions Within Blackboard  

Blackboard supports a ‘Calculated Formula Question’ function, facilitating creation of calculation-based questions using ‘individual variables’ instead of discrete numbers. Figure 1 exemplifies a question that I programmed using ‘variables’. 

Figure 1. An example calculation question in Blackboard. Calculatable variables are presented in blue with square brackets.

Blackboard also permits users to ‘programme in’ the full equation that answers the question – see Figure 2.

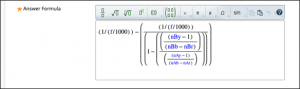
Figure 2. The equation ‘programmed’ into Blackboard which answers the question from Figure 1. Calculatable variables are shown in blue.

Blackboard also specifies important ‘answer-related’ options that can be selected to align with how learners must provide their final answer; e.g. the number of required decimal places, as well as defining how many different ‘answer sets’ should be created for each question – see Figure 3.

 

 

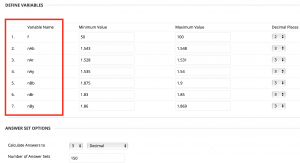
Figure 3. An example of the ‘options’ for the seven variables defined in the question/equation (see Figures 1 and 2). This includes the maximum and minimum values for each variable, the number of decimal places each value is presented to within the question, the number of decimal places required for the final answer, and the number of different ‘answer sets’ programmed for each question.

A sample of the individual variable values and their associated final answers is shown in Figure 4, highlighting that each calculation question can be programmed into Blackboard to generate different sets of variable values, resulting in different final answers. To ensure each student sees a different question from their peers (thereby minimising collusion), programmers must ensure that the number of ‘answer sets’ for each individual question matches the number of students taking the assessment.

 

Figure 4. Nine examples (NB: ‘answer sets’ are organised in ‘rows’) of seven different variables (see column titles) and their corresponding ‘calculated answers’ via the equation in Figure 2. Although this image only shows nine ‘answer sets’, any required number can be programmed.

Once all the desired calculation questions have been ‘programmed in’, an ‘assessment’ can be created anywhere within Blackboard, permitting importation of these questions.

Figure 5 displays some crucial options to further minimise collusion, including a timer function limiting how long students have to complete their SA. Immediately upon this time-limit’s expiry, the assessment is ‘automatically’ submitted.

 

 

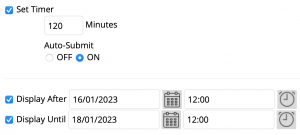
Figure 5. An example of the timer settings, display dates and times that can be programmed into the assessment.

 

Incorporating Disability Advisory Support Service (DASS) requests:

Students receiving DASS-recommended support can be easily assisted using this assessment format. Figure 6 exemplifies how two anonymised students were permitted to complete their SAs within 150 mins (support of 25% extra time) rather than 120 mins.

 

 

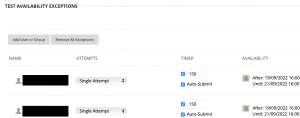
Figure 6. An example of the ‘test availability exceptions’ settings available to programmers.

Finally, Figure 7 highlights the crucial settings of:

• Randomising the order of the questions,
• Ensuring that each question is presented one at a time only, and
• Prohibiting backtracking.

I endorse all three options, as they collectively reduce the risk of collusion.

 

 

 

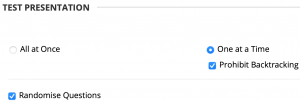
Figure 7. An example of the crucial options which relate to the presentation of the assessment.

 

Conclusion

My innovative approach demonstrates a sophisticated method of creating calculation-based SAs that are robust to collusion. Our external examiners provided extremely positive feedback about this approach for my on-line SAs, which included the following comments:

“I thought your approach to on-line assessments, and in particular how you managed to safe-guard against collusion, was novel and inspired. I like the idea of providing different questions for each student …”

Prof Loffler (Glasgow Caledonian University)

 

“Excellent paper. I REALLY like the idea of changing the values – super! … well done and great to see.”

Prof Allen (Anglia Ruskin University)

 

“This is a fantastic concept … It is very innovative and I don’t recall having seen anything like it before. I do agree that this approach will remove any prospect of academic misconduct.”

Dr Hamilton-Maxwell (Cardiff University)

 

Further Reading:

Amit has also written for Times Higher Education’s Campus+ on  Intended Learning Outcomes, which you can check out below:

https://www.timeshighereducation.com/campus/intended-learning-outcomes-ilos-sideshow-teaching-tool 

If you are interested in also contributing to Times Higher, please fill in the below survey, and we can organise submission of your content:

https://www.qualtrics.manchester.ac.uk/jfe/form/SV_8J3W59DtAZ1kqz4 

Related